Die Mechanismen und Modellierung der Infektionsausbreitung
Was nutzen Pandemiemodelle?
Der folgende Text wendet sich an Leser, die die Mechanismen der Ausbreitung einer Infektionserkrankung verstehen möchten. Ich habe versucht, die Zusammenhänge so einfach, wie möglich darzustellen. Zum Verständnis reichen die Mathematikkenntnisse eines Oberschülers aus.
Dynamische Modelle der Infektionsausbreitung
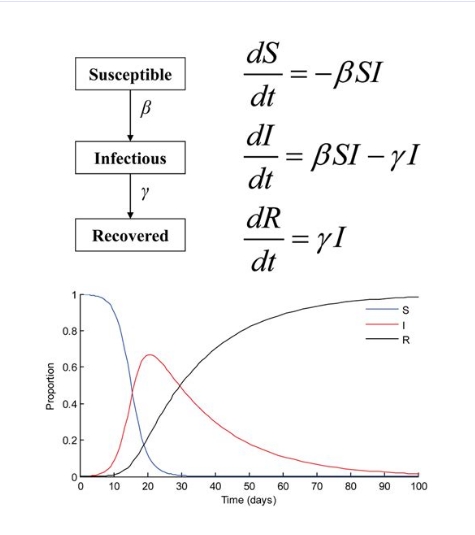
Das bekannteste Modell ist das SIR-Modell, das oben rechts auf der Seite abgebildet ist. Es wurde bereits 1927 erstellt. Die Zusammenhänge sind als Differentialgleichungen formuliert. Die Änderungen der Größen sind in einer Differentialgleichung von den Größen selbst abhängig und nicht von externen Einflüssen. Analytisch lösbar sind nur eine bestimmte Klasse von Differentialgleichungen, nämlich die, deren Zeitfunktion asymptotisch oder periodisch sind. Es ist deswegen einfacher, die Differentialgleichungen zu Differenzengleichungen umzuformen und sie iterativ mit dem Computer zu lösen.
Dabei berechnet man die dynamische Entwicklung in der Zeit in kleinen Schritten, indem das Ergebnis einer Rechnung (Output) wieder als Input in die Formel eingegeben wird. Während bei einer analytischen Lösung nur der gewünschte Zeitpunkt in die Formel eingegeben werden muss und man sofort ein Ergebnis erhält, muss der Systemzustand zu einem gewünschte Zeitpunkt bei der numerischen Lösung durch eine Abfolge immer gleicher Rechenschritte mit einem definierten Zeitintervall Schritt für Schritt berechnet werden. Ohne Computer ist das eine Sysiphusarbeit.
Der Nachteil des Verfahrens ist die erforderliche Rechenkapazität, was aber mit den heute verfügbaren Computern kein Problem mehr ist. Der Vorteil ist, dass sich auch alle analytisch lösbaren Differentialgleichungen mit beliebiger Genauigkeit viel einfacher lösen lassen. Da es zur Zeit der Entstehung des SIR-Modells noch keine Computer gab, konnte man das Problem nur durch Differentialgleichungen lösen.
Für alle Modelle müssen Vereinfachungen gemacht werden. Im Fall eines Infektionsmodells wird die Bevölkerung als homogen verteilt angenommen, obwohl die Bevölkerungsdichte und Kontakthäufigkeit in Großstädten und ländlichen Gebieten stark differiert. Auch das Ansteckungsrisiko muss für alle gleich angesetzt werden. Darüberhinaus gelten alle Modelle nur für den Fall, dass keinerlei Maßnahmen getroffen, wie z.B. Kontaktbeschränkungen. Will man Maßnahmen, wie Kontaktbeschränkungen, Maskentragen oder Ausgangssperren modellieren, so müssen immer mehr Parameter in die Gleichungen eingeführt werden, die man schätzen muss und kaum messen kann. So gibt es manche Modellierer, die versuchen die Reproduktionszahl weiter aufzuschlüsselen und dabei die Kontakthäufigkeit und Kontaktdauer zu implementieren. Doch wie soll man einen Kontakt definieren? Beginnt ein Kontakt erst mit 1,50 Meter Abstand oder näher? Muss die Kontaktperson husten oder niesen, damit es zur Übertragung kommt? Oder genügt ein Gespräch im Abstand von 50 cm und 15 Minuten oder müssen es 100 cm und 30 Minuten sein?
Ich halte ein solches Unterfangen für sinnlos. Ebenso sinnlos dürfte es sein, das Infektionsgebiet nach Bevölkerungsdichte aufzuteilen und dann eventuell noch die Perlokationstheorie eizubauen. Das Resultat ist noch mehr Unsicherheit und unzuverlässige Ergebnisse. Das ich mit dieser Behauptung richtig liege, zeigen die Ergebnisse des englischen Modellierers Neil Ferguson, der mit seinen Prognosen hinsichtlich der Todeszahlen bei der Sars2-Pandemie um den Faktor 100 danebenlag.
Ähnliches dürfte auch für Klimamodelle zutreffen, bei denen oft bis zu 80 Parameter geschätzt werden müssen. Zur Vorhersage sind mathematische Modelle bei komplexen nichtlinearen Prozessen nicht geeignet. Sie können lediglich zum besseren Verständnis dienen und eine worst case Abschätzung ermöglichen.
Besser als das SIR-Modell ist das SEIR-Modell. Während im SIR-Modell jeder Infizierte gleichzeitig auch ansteckend ist und daher seine Infektion ohne Zeitverzug sofort weitergibt, berücksichtigt das SEIR-Modell auch die Inkubationszeit. Während dieser Zeitspanne ist der Infizierte noch nicht infektiös aber kann im Modell bereits als immun gelten, genauer gesagt als nicht mehr suszeptibel. Das Modell beschreibt daher den Ablauf von Infektion und Infektiosität besser als das SIR-Modell. Gut erklärt wird das Modell bei Wikipedia.
Ich habe deshalb das SEIR-Modell in Excel implementiert. Das File kann hier heruntergeladen werden.
SEIR-Modell
Dabei berechnet man die dynamische Entwicklung in der Zeit in kleinen Schritten, indem das Ergebnis einer Rechnung (Output) wieder als Input in die Formel eingegeben wird. Während bei einer analytischen Lösung nur der gewünschte Zeitpunkt in die Formel eingegeben werden muss und man sofort ein Ergebnis erhält, muss der Systemzustand zu einem gewünschte Zeitpunkt bei der numerischen Lösung durch eine Abfolge immer gleicher Rechenschritte mit einem definierten Zeitintervall Schritt für Schritt berechnet werden. Ohne Computer ist das eine Sysiphusarbeit.
Der Nachteil des Verfahrens ist die erforderliche Rechenkapazität, was aber mit den heute verfügbaren Computern kein Problem mehr ist. Der Vorteil ist, dass sich auch alle analytisch lösbaren Differentialgleichungen mit beliebiger Genauigkeit viel einfacher lösen lassen. Da es zur Zeit der Entstehung des SIR-Modells noch keine Computer gab, konnte man das Problem nur durch Differentialgleichungen lösen.
Für alle Modelle müssen Vereinfachungen gemacht werden. Im Fall eines Infektionsmodells wird die Bevölkerung als homogen verteilt angenommen, obwohl die Bevölkerungsdichte und Kontakthäufigkeit in Großstädten und ländlichen Gebieten stark differiert. Auch das Ansteckungsrisiko muss für alle gleich angesetzt werden. Darüberhinaus gelten alle Modelle nur für den Fall, dass keinerlei Maßnahmen getroffen, wie z.B. Kontaktbeschränkungen. Will man Maßnahmen, wie Kontaktbeschränkungen, Maskentragen oder Ausgangssperren modellieren, so müssen immer mehr Parameter in die Gleichungen eingeführt werden, die man schätzen muss und kaum messen kann. So gibt es manche Modellierer, die versuchen die Reproduktionszahl weiter aufzuschlüsselen und dabei die Kontakthäufigkeit und Kontaktdauer zu implementieren. Doch wie soll man einen Kontakt definieren? Beginnt ein Kontakt erst mit 1,50 Meter Abstand oder näher? Muss die Kontaktperson husten oder niesen, damit es zur Übertragung kommt? Oder genügt ein Gespräch im Abstand von 50 cm und 15 Minuten oder müssen es 100 cm und 30 Minuten sein?
Ich halte ein solches Unterfangen für sinnlos. Ebenso sinnlos dürfte es sein, das Infektionsgebiet nach Bevölkerungsdichte aufzuteilen und dann eventuell noch die Perlokationstheorie eizubauen. Das Resultat ist noch mehr Unsicherheit und unzuverlässige Ergebnisse. Das ich mit dieser Behauptung richtig liege, zeigen die Ergebnisse des englischen Modellierers Neil Ferguson, der mit seinen Prognosen hinsichtlich der Todeszahlen bei der Sars2-Pandemie um den Faktor 100 danebenlag.
Ähnliches dürfte auch für Klimamodelle zutreffen, bei denen oft bis zu 80 Parameter geschätzt werden müssen. Zur Vorhersage sind mathematische Modelle bei komplexen nichtlinearen Prozessen nicht geeignet. Sie können lediglich zum besseren Verständnis dienen und eine worst case Abschätzung ermöglichen.
Besser als das SIR-Modell ist das SEIR-Modell. Während im SIR-Modell jeder Infizierte gleichzeitig auch ansteckend ist und daher seine Infektion ohne Zeitverzug sofort weitergibt, berücksichtigt das SEIR-Modell auch die Inkubationszeit. Während dieser Zeitspanne ist der Infizierte noch nicht infektiös aber kann im Modell bereits als immun gelten, genauer gesagt als nicht mehr suszeptibel. Das Modell beschreibt daher den Ablauf von Infektion und Infektiosität besser als das SIR-Modell. Gut erklärt wird das Modell bei Wikipedia.
Ich habe deshalb das SEIR-Modell in Excel implementiert. Das File kann hier heruntergeladen werden.
SEIR-Modell
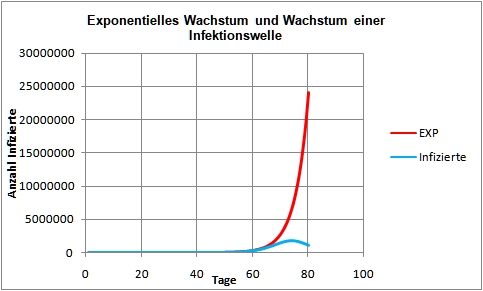
Ein einfaches diskretes Modell der Infektionsausbreitung